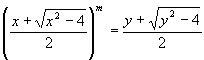
|
350088 г. Краснодар ул Сормовская, 203 |
КРАЕВАЯ ОЛИМПИАДА ПО МАТЕМАТИКЕ |
1 .Показать, что уравнения a
x = x и2. В выпуклом шестиугольнике ABCDEF каждая из диагоналей AD, BE и CF делит его на два равновеликих четырехугольника. Известно, что прямая AD делит отрезок BE в отношении 1998 : 1999. В каком отношении эта прямая делит отрезок CF?
3. Два игрока играют в следующую игру: сначала на доске написаны числа 2, 4, 6, 8,…, 1998. За один ход можно уменьшить на 1 любое из написанных чисел. При этом с доски стираются нули и числа, совпадающие с каким-то из уже написанных на доске чисел. Проигрывает тот, после чьего хода на доске не останется ни одного числа. Кто выигрывает при правильной игре?
4.Пусть m - натуральное число, m
і 2. Доказать, что уравнение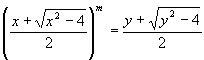
имеет бесконечно много решений в натуральных числах.