с
плотностью С, с вероятностью R
попадает в 
и имеет там плотность 
может быть
равной b1 с вероятностью p1 и b2 с вероятностью p2.Случайная величина и её числовые характеристики (задание по ТР)
Случайная
величина Х равномерно распределена
на с
плотностью С, с вероятностью R
попадает в и имеет там плотность может быть
равной b1 с вероятностью p1 и b2 с вероятностью p2.
Задача: Построить график функции распределения, плотности.
Найти m=M[X], s2= D[X] и s,
.
(Заданы
Пустые
клетки означают необходимость
вычислить.)
Пусть дано:
Требуется найти: C, z3, M[x], s2=D[x], s, P(s)=P{|X-MX|<s}.
Решение
Находим
C из условий F(+
)=1 , т.е. из уравнения
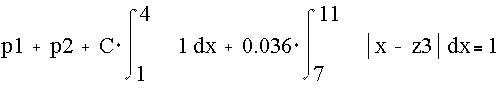
С
учетом условия P{
}=R, тогда получаем
z3
найдем из условия P{}=R,т.е из уравнения
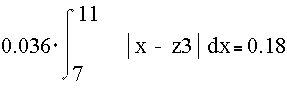
Решая последнее уравнение относительно z3 получаем два корня
Тогда для z31:
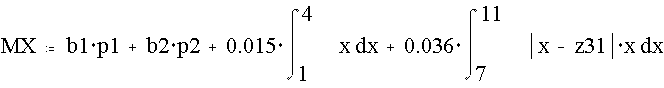
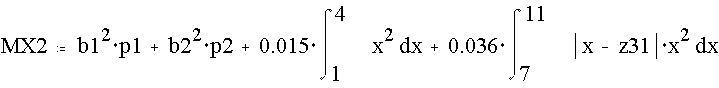
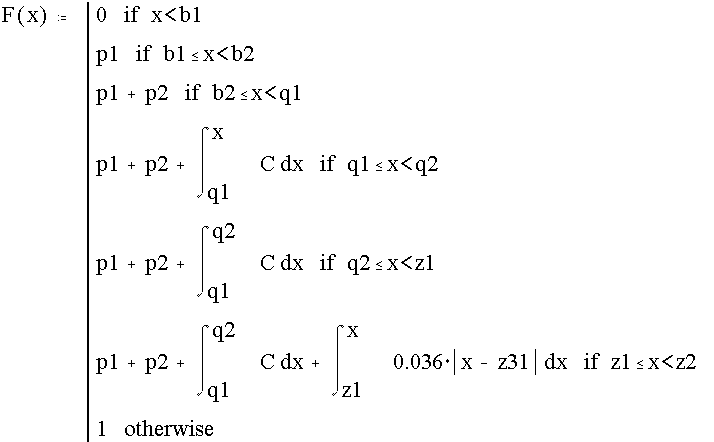
Тогда
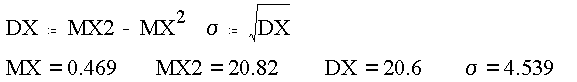
Далее
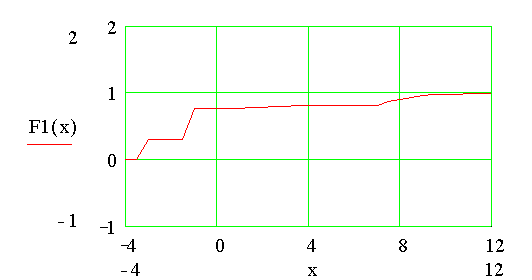
Построим график функции распределения
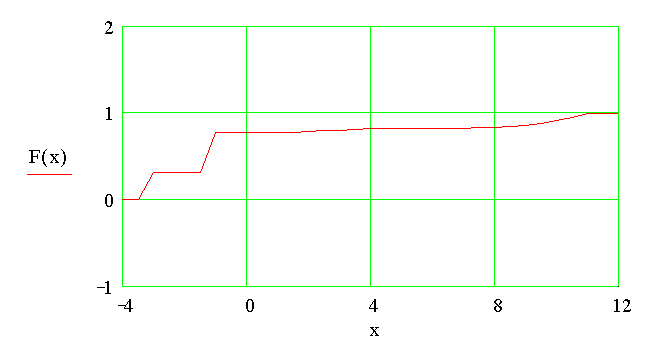
Для z32:
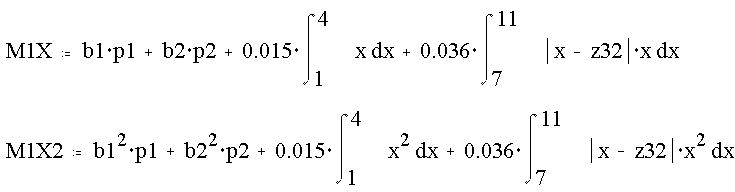
Тогда
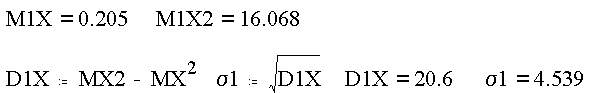
Функция распределения имеет вид
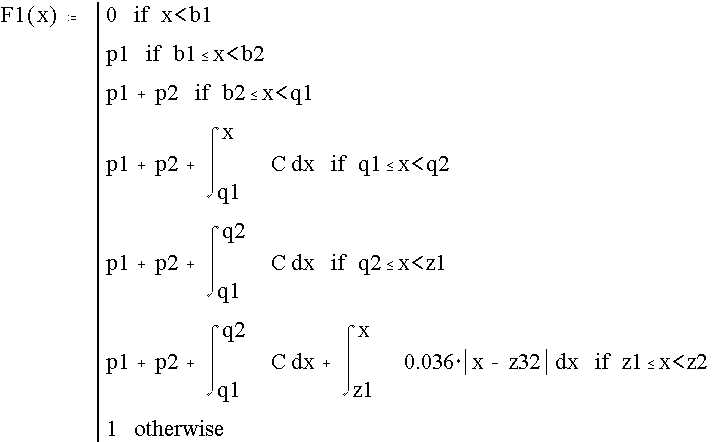
График функции распределения для z32 имеет вид
