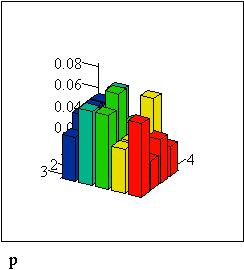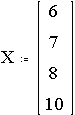
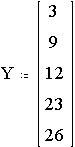
Задача
Заданы случайные величины. Закон распределения случайного вектора (X,Y) задан матрицей р. Требуется:
а) Найти безусловные законы распределения X и Y;
б) установить зависимы они или нет.
в) вычислить вероятность P(X>Y);
г) Найти MX, MY, DX, DY,
sX, sY;д)вычислить ковариацию и коэффициент корреляции;
е) описать условные законы распределения P(X=Xi/Y=Yj). Найти условные математические ожидания M(X/Y=Yj).
Пусть матрица совместного закона распределения p имеет вид:
X\Y |
3 |
9 |
12 |
23 |
26 |
6 |
0,05634 |
0,07042 |
0,04225 |
0,07042 |
0,02817 |
7 |
0,05634 |
0,05634 |
0,01408 |
0,02817 |
0,04225 |
8 |
0,05634 |
0,02817 |
0,08451 |
0,04225 |
0,02817 |
10 |
0,04225 |
0,07042 |
0,07042 |
0,04225 |
0,07044 |
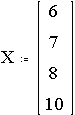
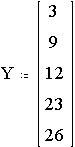
![]()
![]()
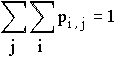
Случайные величины X и Y определены соотношениями:
Их совместное распределение определяется матрицей р, Р{X=xi,Y=yj}=pi,j.
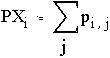
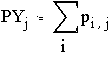


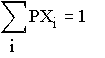
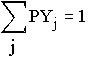
![]()
б) Условие независимости имеет вид pi,j= PXI*PYJ при всех i и j.
![]()
![]()
Вывод: Случайные величины зависимы.
в) Вычислим Q=P[X>Y}
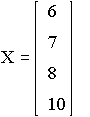
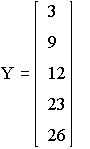
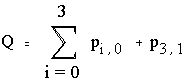
Следовательно:
![]()
г) Найдем матожидание и дисперсии.
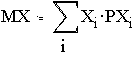
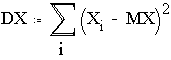
Имеем: ![]()
![]()
![]()
Далее, т.к.
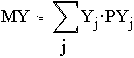
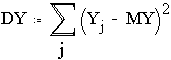
то
д) Найдем ковариацию K=cov(XY)=M(X-MX)*(MY-MY)=MXY-MX*MY и коэффициент корреляции
r=K/(sX*sY).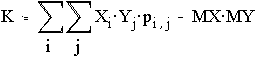
![]()
![]()
![]()
е) Опишем условный закон распределения Pi,j=P(X=xi/Y=yj)
Пусть
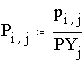 тогда
тогда 
Найдем условные математические ожидания
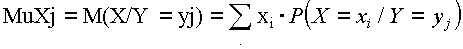
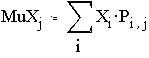

Опишем условный закон распределения Qi,j=P
(Y=yj/X=xi)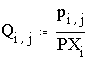

Найдем условные математические ожидания MuYi=M(Y/X=xi)
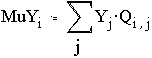

Совместная функция распределения определяется по формуле
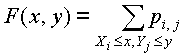
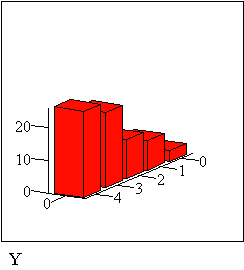
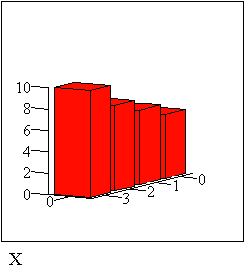
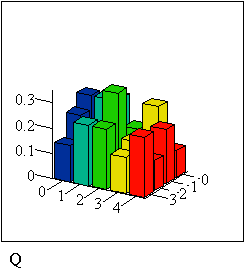
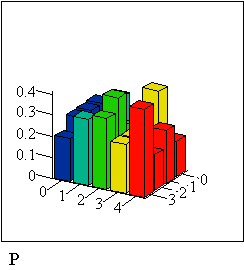
Построим гистограммы совместного закона распределения p и условных распределений
P, :