Геометрические вероятности.

Существуют эксперименты, исходы которых нельзя описать с помощью конечных пространств элементарных событий. В этих случаях иногда бывает полезным понятие геометрической вероятности.

Пусть пространством W элементарных событий некоторого эксперимента является часть числовой прямой или часть плоскости, или часть пространства, имеющая конечную меру m(W ). Под мерой множества понимается длина, площадь и объем соответственно. Случайным событием А называется такое подмножество пространства W , которое имеет конечную меру m(W ). Тогда вероятность Р(А) события А определяется равенством (геометрическая вероятность).

Этот метод вычисления вероятности применяется тогда, когда по условиям эксперимента вероятность появления элементарного события (точки пространства W ) во множестве А пропорциональна мере множества А и не зависит от его расположения в пространстве W . В таком случае говорят, что случайная точка имеет равномерное распределение в пространстве W .

Д Пример На окружности единичного радиуса случайным образом ставятся три точки А, В и С. Найти вероятность того, что треугольник АВС остроугольный.

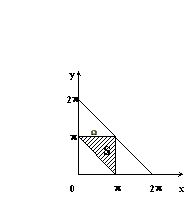
Будем измерять длины дуг единичной окружности между точками в таком направлении, чтобы при движении по окружности за точкой А следовала точка В, а за точкой В - точка С. Обозначим через х - длину дуги АВ, через у - длину дуги ВС. Тогда различным исходам рассматриваемого эксперимента можно сопоставить точки плоскости ХОY с координатами х и у, удовлетворяющими неравенствам то есть, .

Если событие S - треугольник АВС остроугольный, то .

Очевидно, площадь области W равна 2p ², а площадь области S равна . См. рис. 1. Следовательно, вероятность . Г

Задачи Параметры Ответы Примеры Решение

Случайные события