Тогда исходы опыта называют элементарными событиями, а их совокупность W называют пространством элементарных событий.

Любое случайное событие А, которое может произойти в опыте, состоит из элементарных событий некоторого пространства W элементарных событий, то есть является подмножеством пространства W . Само пространство W является событием, которое всегда наступает в опыте и называется достоверным. Пустое подмножество пространства W является событием, которое никогда не наступает в рассматриваемом опыте. Это событие называется невозможным и обозначается символом Ж .

Пусть W = { w ₁; w ₂ ; ... w _n } - некоторое пространство элементарных событий соответствующих какому-то эксперименту. Каждому элементу w _i из W поставим в соответствие неотрицательное число p_i так, что p₁+p₂+...+p_n=1. Выбор чисел p_i происходит, как правило, исходя из сравнения возможностей различных исходов эксперимента. Число p_i называется вероятностью элементарного события w _i . Вероятностью любого события А называют число Р( |А| ), равное сумме вероятностей элементарных событий , составляющих А. При этом, если событие А не содержит элементов, то вероятность Р( А ) = 0.

Предположим, что по условиям опыта все элементарные события равновозможные, то есть каждое элементарное событие не имеет никаких преимуществ в появлении по сравнению с остальными элементарными событиями. Тогда имеет смысл считать, что р(w ₁)=р(w ₂)=...=р(w _n) и, следовательно, р( w _i )= . Обозначим через - число элементов конечного множества А. Если событие А содержит k элементарных событий, то р(А)=. Это определение вероятности события называется классическим.

Для вычисления вероятности по классическому определению необходимо находить число элементов в пространстве элементарных событий W и в различных случайных событиях - подмножествах W . Это часто удается сделать, используя комбинаторные методы. Большинство комбинаторных задач решается с помощью следующих двух основных принципов.

Принцип умножения. Если множество А содержит n элементов, а множество В содержит K элементов, то множество всех различных упорядоченных пар вида (a;b), где содержит n ^. k элементов.

Принцип сложения. Если множество С можно разбить на два непересекающихся подмножества А и В, множество А содержит n элементов, множество В содержит k элементов, то множество содержит n+k элементов.

Множество, состоящее из n элементов, называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое натуральное число ( номер элемента ) от 1 до n. Упорядоченные множества считаются различными, если они отличаются друг от друга либо своими элементами, либо их порядком.

Упорядоченные k-элементные подмножества из n элементов называются размещениями из n элементов по k. Число различных размещений из n элементов по k обозначается . Используя принцип умножения легко показать, что

где n!=1^.2^. ... ^.n (0!=1).

Любое k-элементное подмножество множества из n элементов называется сочетанием из n элементов по k. В отличие от размещений сочетания являются неупорядоченными подмножествами и поэтому различаются только своими элементами. Число всех различных сочетаний из n элементов по k обозначается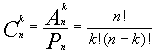 или . Любое размещение из n элементов по k можно получить двумя последовательными действиями : а - выбор сочетания из n элементов по k; b - расстановка k элементов выбранного сочетания в определенном порядке. Очевидно, число всех различных размещений из n элементов по k равно числу всех упорядоченных пар вида ( a, b ) и равно . Следовательно,

.

 Существуют эксперименты, исходы которых нельзя описать с помощью конечных пространств элементарных событий. В этих случаях иногда бывает полезным понятие геометрической вероятности.

Пусть пространством W элементарных событий некоторого эксперимента является часть числовой прямой или часть плоскости, или часть пространства, имеющая конечную меру m(W ). Под мерой множества понимается длина, площадь и объем соответственно. Случайным событием А называется такое подмножество пространства W , которое имеет конечную меру m(W ). Тогда вероятность Р(А) события А

Этот метод вычисления вероятности применяется тогда, когда по условиям эксперимента вероятность появления элементарного события (точки пространства W ) во множестве А пропорциональна мере множества А и не зависит от его расположения в пространстве W . В таком случае говорят, что случайная точка имеет равномерное распределение в пространстве W .