

ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Функцией-оригиналом называется комплекснозначная функция f (t) действительного аргумента t, удовлетворяющая условиям:
1. f (t) интегрируема на любом конечном интервале оси t;
2. f (t)=0 для всех отрицательных t;
3. f (t) возрастает не быстрее показательной функции, т. е. существуют такие постоянные М и s0, что |f(t)|<Mes0t для всех t.
Изображением функции f (t) (по Лапласу) называется функция F(p) комплексного переменного p=s +it , определяемая равенством
 .
.
Тот факт, что F(p) есть изображение f (t), будем символически записывать так:
![]() .
.
Для любой функции-оригинала f (t) изображение определено в полуплоскости Rep>s0 и является в этой полуплоскости аналитической функцией.
Из определения изображения следуют его простейшие свойства:
1. Линейность. Для любых комплексных постоянных a и b
![]()
(здесь и далее считать f(t)=F(p), g(t)=G(p)).
2.Теорема подобия. Для любого постоянного a >0
 .
.
3. Дифференцирование оригинала. Если функции f (t), fў (t) , fІ (t),…, f (n)(t) являются функциями-оригиналами и f(t)=F(p), то
![]() ,
,
![]() ,
,
![]() ,
,
где под f (k)(0),
(k= 1, 2,…, n-1) понимается
![]() .
.
4. Дифференцирование изображения. Дифференцирование изображения сводится к умножению на (-t) оригинала
![]()
или вообще
![]() .
.
5. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р, т. е. если f(t)=F(p), то
 .
.
6. Интегрирование
изображения. Если интеграл
 сходится,
то он служит изображением функции
сходится,
то он служит изображением функции![]()
 .
.
7.Теорема смещения. Если f(t)=F(p), то для любого комплексного р0
![]() .
.
8.Теорема запаздывания. Если f(t)=F(p), то для любого t >0
![]() .
.
Важной для приложений является следующая:
Теорема единственности
Если две функции j(t) и j(t) имеют одно и то же L-изображение F(p), то эти функции тождественно равны.
Роль теоремы в том, что, если при решении практической задачи мы каким-либо образом определили изображение искомой функции, а потом по изображению нашли начальную функцию, то на основании теоремы единственности мы заключаем, что найденная функция есть решение поставленной задачи и других решений не существует.
Применяя определения 1, 2, и указанные выше свойства, получаем таблицу изображений основных элементарных функций (см. приложение).
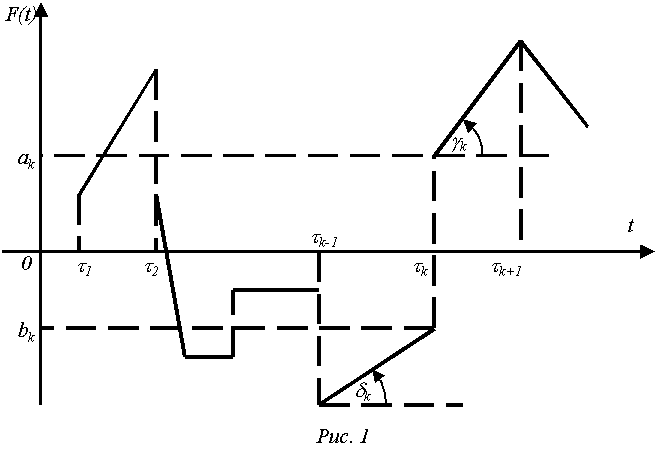
Используя определение преобразования Лапласа, нетрудно вывести формулу для изображения кусочно-линейной функции. Примерный вид графика кусочно-линейной функции приведен на рис. 1.
Введем обозначения:
tk – точки разрыва функции f (t) или fў (t);
a k =ak–bk – скачки функции в узлах “стыка”;
bk=tggk– tgdk – скачки производной fў (t) в узлах “стыка”.
Изображение кусочно-линейной функции имеет вид
 .
.

Можно получить изображение кусочно-линейной функции непосредственной подстановкой ее уравнения в формулу из определения.
В некоторых случаях бывает удобно применить теорему запаздывания.