ТЕОРИЯ
а)
Найти вычет функции: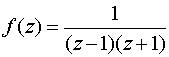
в точке z=1.
Решение. Воспользуемся первой формулой п. 2. из списка основных формул для нахождения вычетов:
.
б) Найти вычеты функции f (z)=tgz в ее особых точках.
Решение. Особые точки функции tgz – нули ее знаменателя, т. е. точки
,
k=0, ± 1, ± 2, …
есть полюса первого порядка.
Воспользуемся второй формулой п.2. Пусть j (z)=sinz, y (z)=cosz. Тогда
.
в)
Найти вычет функции 
в особой
точке z=0.
Решение. В точке z=0 имеем
.
Следовательно,
точка z=0 есть устранимая особая точка функции f (z).
Поэтому 
.
г)
Найти вычет функции 
в точке
z=2.
Решение.
В точке z=2 функция имеет
полюс второго порядка.
Из п. 3 имеем
.
д)
Найти вычет функции 
в точке
z=0.
Решение.
Функция 
разлагается в окрестности
особой точки z=0 в ряд Лорана:
.
Следовательно, по теореме
.
е)
в бесконечно удаленной точке.
Решение.
Функция 
при |z|>1
разлагается в ряд Лорана
.
Следовательно по теореме
.
