Двойные интегралы
I. Вычисление двойных интегралов с помощью двойного интегрирования.
Пример 1. Пример 2. Пример 3 Пример4.
II. Замена переменной в двойном интеграле.
Двойные интегралы обладают такими же свойствами, как и определённые интегралы (линейность, аддитивность, формулы среднего значения и т.д.).
I. Вычисление двойных интегралов с помощью двойного интегрирования.

имеет место формула
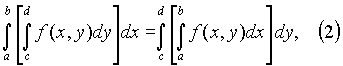
которая показывает, что порядок интегрирования можно менять.
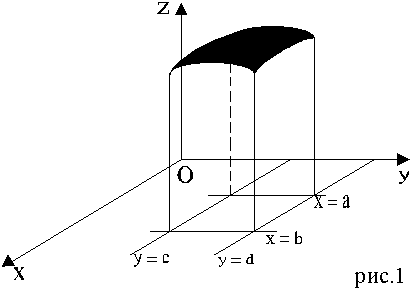
Интеграл (1) представляет собой объём тела, ограниченного снизу прямоугольником P, сбоку - боковыми гранями прямой призмы, построенном на этом прямоугольнике, а сверху - той частью поверхности, которая вырезана этой призмой (рис. 1).
2. Если функция f(x,
y) непрерывна на
множестве ![]()
где ![]() и
и ![]() непрерывны
на отрезке [a, b] и
непрерывны
на отрезке [a, b] и ![]() на [a,
b]
на [a,
b]
(рис. 2), то
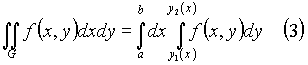
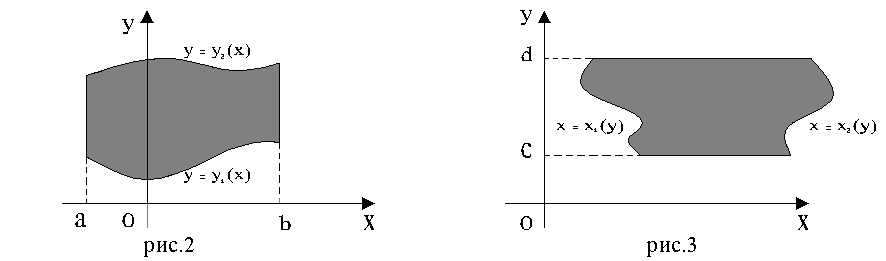
Правая часть в (3) называется повторным интегралом, то есть результатом последовательного вычисления сначала интеграла по y при фиксированном x, а затем интеграла по x от получившейся функции.
3. Если функция f(x,
y) непрерывна в области
G (рис. 3), ![]()
где функции ![]() и
и ![]() непрерывны на сегменте [c, d] и
непрерывны на сегменте [c, d] и ![]() на [c, d], то верно равенство
на [c, d], то верно равенство
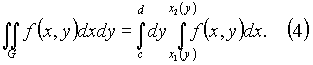
4. Если область G такова (рис. 4), что к ней применима и формула (3) и формула (4), то
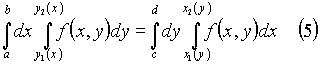
Это равенство используется для перемены порядка интегрирования в повторном интеграле.
Области более сложного вида следует разбить на части, к которым применима формула (3) или (4).
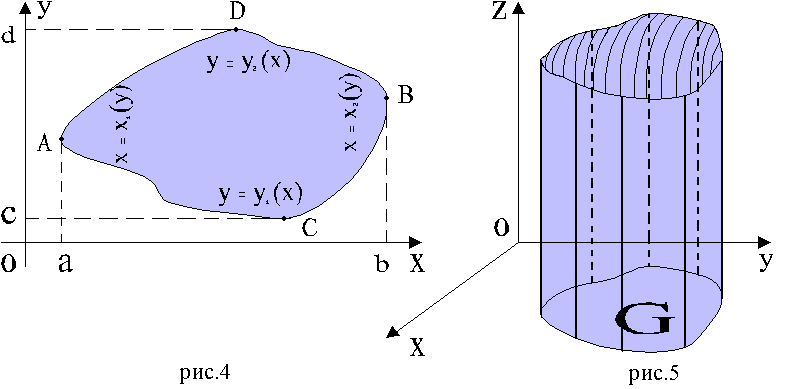
Двойной интеграл  представляет
собой объём
представляет
собой объём
цилиндрического бруса - тела, ограниченного сверху поверхностью z= f(x, y), с боков цилиндрической поверхностью с образующими, параллельными оси z, снизу - фигурой G на плоскости xy (рис. 5).
Пример 1. Измерить порядок интегрирования в интеграле
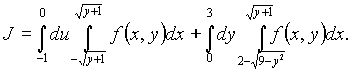
Решение. В рассматриваемом примере следует начинать с построения области интегрирования, поскольку интегралы заданы с указанием порядка интегрирования и пределов по соответствующим переменным. Напомним, что переменные пределы интегрирования внутреннего интеграла являются границами изменения x при фиксированном y. Поэтому область интегрирования G1 для первого интеграла можно задать неравенствами
![]() где
где ![]() и
и ![]() представляют
собой дуги параболы
представляют
собой дуги параболы ![]() лежащие
ниже оси Ox. Область интегрирования во втором
интеграле имеет вид
лежащие
ниже оси Ox. Область интегрирования во втором
интеграле имеет вид
![]() где кривые
где кривые ![]() и
и ![]() представляют собой дуги
параболы
представляют собой дуги
параболы ![]() и дугу окружности
и дугу окружности ![]() лежащие выше оси Ox.
лежащие выше оси Ox.
Пусть G = G1UG2 (рис. 6). Тогда каждая прямая x = const, ![]() пересекает
множество G по отрезку с концами
пересекает
множество G по отрезку с концами ![]() и
и ![]()
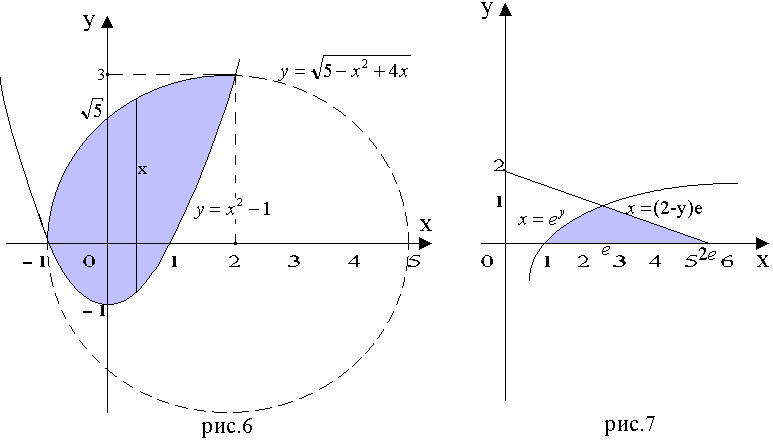
Следовательно, область G можно представить в виде
![]()
А, значит,
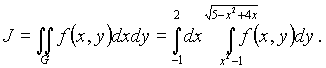
Заметим, что перемена порядка интегрирования в повторном интеграле иногда существенно упрощает его вычисление.
Пример 2. Вычислить интеграл
 где область G ограничена линиями:
где область G ограничена линиями:
 и у = 0 (рис.7).
и у = 0 (рис.7).
Решение. При каждом
фиксированном значении y,![]() значение x меняется от
значение x меняется от ![]() до x = (2 - y) e. Поэтому
до x = (2 - y) e. Поэтому
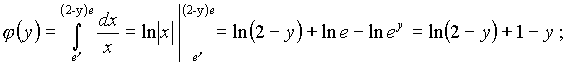
Интегрируя теперь функцию ![]() по y в пределах от y = 0 до y = 1, получим
по y в пределах от y = 0 до y = 1, получим
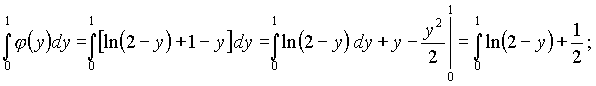
При вычислении интеграла
 используем форму интегрирования по
частям. Имеем
используем форму интегрирования по
частям. Имеем
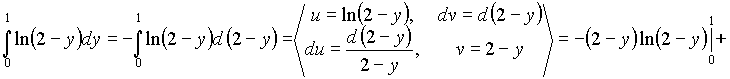
 Итак,
Итак, 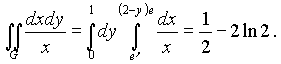
Пример 3. Вычислить объём тела, ограниченного поверхностями
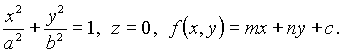
Решение. Область интегрирования G имеет вид (рис. 8).
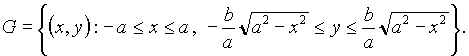
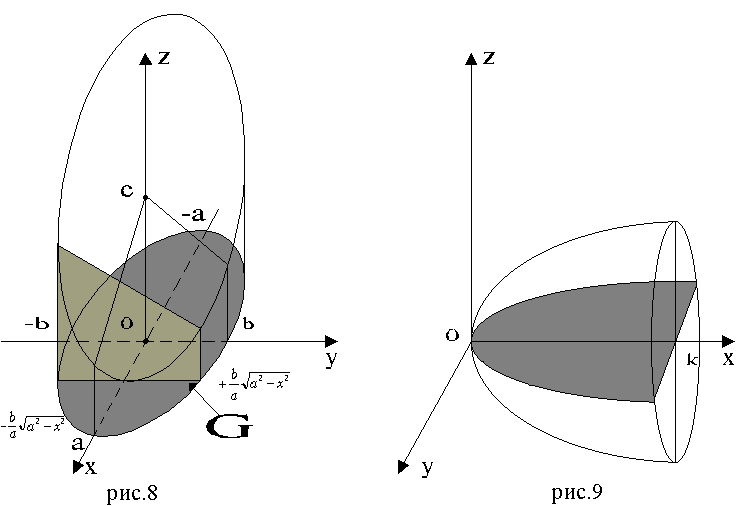
Согласно формуле (3) имеем
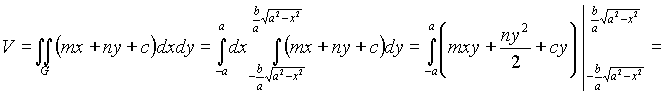
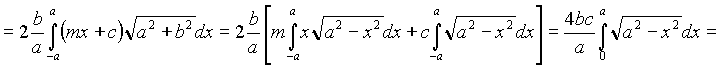
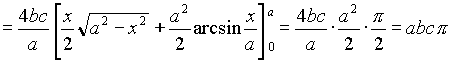
Пример4.
Вычислить объём тела, отсекаемого от
эллиптического параболоида  плоскостью x = k (k > 0) (рис. 9).
плоскостью x = k (k > 0) (рис. 9).
Решение. В каждом из четырёх октантов, где x положительно, находится четвёртая часть тела. Исходя из этого, получаем
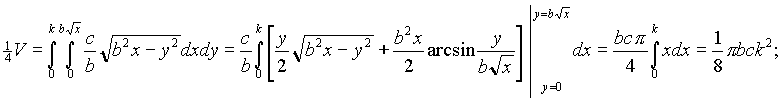
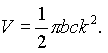
II. Замена переменной в двойном интеграле.
Замена переменной в
интеграле  состоит
в переходе переменных x и y к новым переменным u и v, связанных со старыми соотношениями
состоит
в переходе переменных x и y к новым переменным u и v, связанных со старыми соотношениями
![]()
Если выполняются условия:
1°. Отображение (6) взаимно однозначно.
2°. Функция в (6) непрерывно - дифференцируемы в области D.
3°. Якобиан отображения (6)
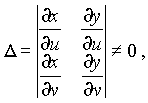
то имеет место формула
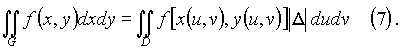
Обычно замена переменных производится с целью упрощения области интегрирования. Соотношения (6) называют переходом от прямоугольных декартовых координат к криволинейным.
Примером криволинейных
координат являются полярные координаты ![]() связанные с прямоугольными (x, y) формулами
связанные с прямоугольными (x, y) формулами
![]()
Якобиан преобразования (8) равен
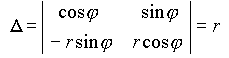
Если ![]() то
то
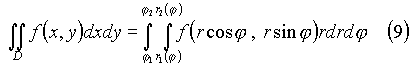
Используются также обобщение полярные координаты. В качестве примера вычислим объём тела заданного в примере 3 (второй способ).
Решение. Введём обобщение
полярные координаты ![]() Тогда
Тогда
![]()
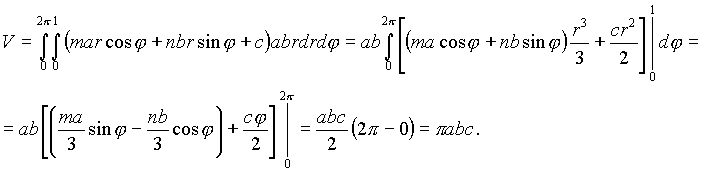
Площадь S квадрируемой области G в плоскости xy находится по формуле
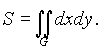
Переходя к криволинейным координатам, получим
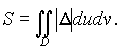
Величину dxdy называют элементом площади в
прямоугольных координатах; ![]() - элементом площади в
криволинейных координатах;
- элементом площади в
криволинейных координатах; ![]() - элемент площади в полярных координатах.
- элемент площади в полярных координатах.
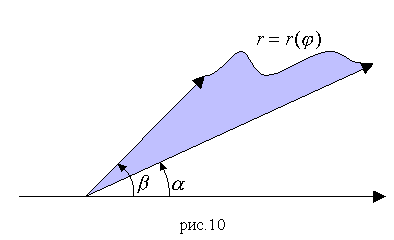
Пусть D - криволинейный
сектор, ограниченный лучами: ![]() и кривой
и кривой ![]() - полярные
координаты (рис. 10). Тогда
- полярные
координаты (рис. 10). Тогда
 известная вормула.
известная вормула.
Пусть G - материальная
пластинка (квадрируемая фигура) на плоскости xy с плотностью ![]()
Тогда
 - масса пластинки;
- масса пластинки;
 -
статические моменты пластинки относительно осей
Ох и Оу;
-
статические моменты пластинки относительно осей
Ох и Оу;
 -
координаты центра тяжести пластинки;
-
координаты центра тяжести пластинки;
![]() -
момент инерции пластинки относительно осей Ох и
Оу;
-
момент инерции пластинки относительно осей Ох и
Оу;
 -
момент инерции пластинки относительно начала
координат.
-
момент инерции пластинки относительно начала
координат.
Пример 5. Пластинка G задана ограничивающими её кривыми:
 -
поверхностная плотность. Найти массу пластинки.
-
поверхностная плотность. Найти массу пластинки.

Решение. Пластинку расположим в прямоугольной системе координат так, чтобы центры окружностей совпадали с началом координат (рис. 11).
Имеем  . Перейдём в
двойном интеграле к полярным координатам
. Перейдём в
двойном интеграле к полярным координатам ![]() При этом область G преобразуется в
прямоугольную область.
При этом область G преобразуется в
прямоугольную область.
 Имеем
Имеем
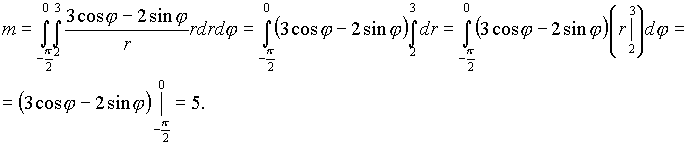
*) этим обеспечено существование всех встречающихся ниже интегралов