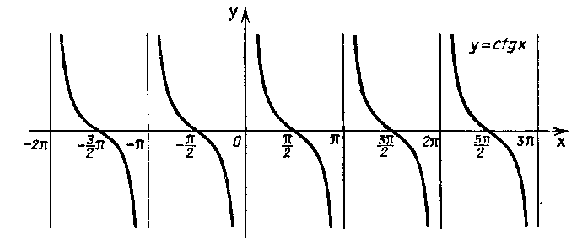Функции
![]()
.
СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
ГРАФИКИ
|
Функции |
|
. |
Для построения графиков данных функций проведем исследование по общей схеме.
|
|
|
|
|
||
|
1. Область определения |
|
|
|
||
|
2. Множество значений |
|
|
|
||
|
3. Периодичность |
Все тригонометрические функции периодические с наименьшим положительным периодом
|
||||
|
4. Четность |
нечетная
|
четная
|
нечетная
|
||
|
5. Нули функции |
|
|
|
||
|
интервалы знакопостоянства
|
|
|
|
||
|
|
|
|
|||
Итоговые таблицы исследования тригонометрических функций и их графики
|
Монотонность, производные тригонометрических функций
|
Зная производные тригонометрических функций
и условие возрастания ( на промежутках, где производная функции положительна) и убывания ( на промежутках, где производная функции отрицательна) функций, составим следующую наглядную таблицу: |
|
y = sinx |
0; p/2 |
p/2 |
p/2; p |
p |
p; 3p/2 |
3p/2 |
3p/2;2p |
2p |
|
|
|
m a x |
|
п е р е г и б |
|
m i n |
|
п е р е г и б |
График функции
y = sinx имеет вид: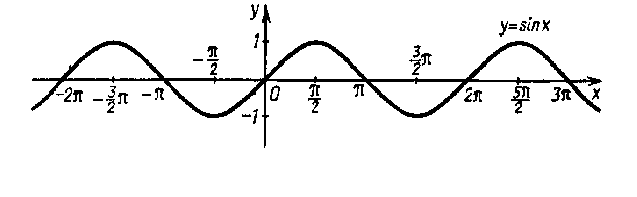
|
y = cosx |
0; p/2 |
p/2 |
p/2; p |
p |
p; 3p/2 |
3p/2 |
3p/2;2p |
2p |
|
|
|
п е р е г и б |
|
m i n |
|
п е р е г и б |
|
m a x |
График функции
y = cosx имеет вид:
|
y = tgx |
-p/2; p/2 |
0 |
0 p/2 |
p /2 |
p /2; p |
p |
p;3p/2 |
3p/2 |
|
|
|
п е р е г и б |
|
Р А З Р Ы В |
|
п е р е г и б |
|
Р А З Р Ы В |
График функции
y = tgx имеет вид:
График функции
y = ctgx имеет вид: